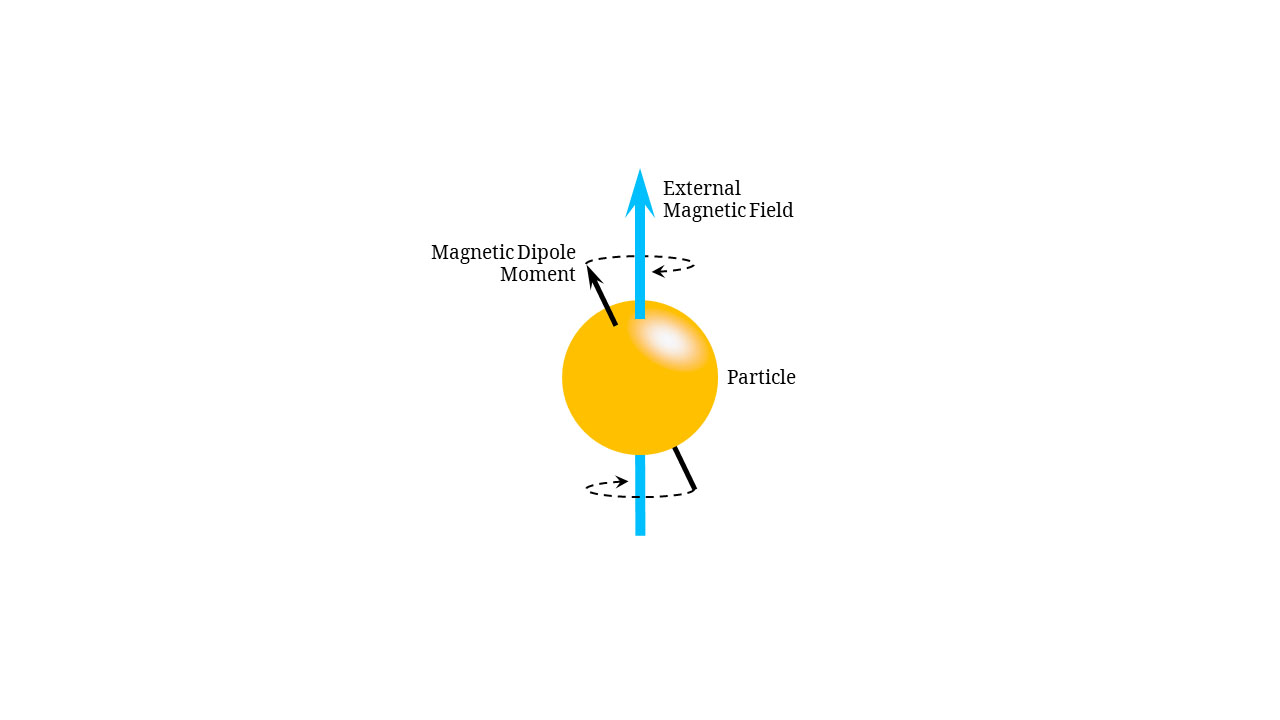
核磁共振，指的是磁矩不为零的原子核在恒定磁场中，由射频电磁场引起塞曼能级之间的共振跃迁现象。1939 年，伊西多·艾萨克·拉比通过试验高温蒸发后的物质发现了核磁共振现象，并因此于 1944 年获得了诺贝尔物理学奖。时至今日，核磁共振已经成为了医学、化学、生物学等多个学科不可或缺的研究手段。

预备知识

在学习核磁共振的基本原理之前，应首先了解本节内容。

原子核的自旋

组成任何原子核的所有核子都具有自旋的量子特性。原子核的自旋角动量的大小 $S$ 可以由自旋量子数 $s$ 表示：

$$S = \hbar \sqrt{s(s+1)}$$

如果某个原子核中的质子和中子的数量都是偶数，那么自旋量子数 $s=0$；如果某个原子核质量数为奇数，那么自旋量子数 $s$ 取半整数；如果某个原子核质量数为偶数，并且质子数为奇数，那么自旋量子数 $s$ 取整数。与沿 $z$ 轴或外加磁场方向，且与自旋分量相关的整数或半整数量子数被称为磁量子数 $m$。磁量子数 $m$ 可以以整数为步长在 $-s$ 到 $+s$ 内取值。因此，对于任何给定的原子核，总共有 $2s + 1$ 个自旋状态（磁量子数）。自旋角动量 $\boldsymbol{S}$ 在 $z$ 方向的分量为：

$$S_z = m\hbar$$

原子核的自旋磁矩

自旋角动量 $\boldsymbol{S}$ 不为零的原子核具有相应的核自旋磁矩 $\boldsymbol{\mu}$，简称为核磁矩。核磁矩的表达式为：

其中，$g$ 为朗德因子，是一个无量纲的量，其数值取决于原子核的结构，它的值可能为正，也可能为负；$\mu_\mathrm{N}$ 为核磁子，在国际单位制下它的定义式为：

$$\mu_\mathrm{N} = \frac{e\hbar}{2m_\mathrm{p}}$$

式中，$e$ 为元电荷，$m_\mathrm{p}$ 为质子的静止质量。核自旋磁矩与自旋角动量的比值称为旋磁比 $\gamma$，其表达式为：

$$\gamma = \frac{g\mu_\mathrm{N}}{\hbar}$$

因此，式 (1) 可改写为：

$$\boldsymbol{\mu} = \gamma \boldsymbol{S}$$

核自旋磁矩 $\boldsymbol{\mu}$ 在 $z$ 方向的分量为：

能级分裂

原子核共有 $2s + 1$ 个自旋状态，对应 $2s + 1$ 个磁量子数。在没有磁场的情况下，这些态是简并的，具有相同的能量。在外加磁场的作用下，由于核自旋磁矩和外加磁场之间的相互作用，这些态不再拥有相同的能量，发生能级分裂。在外磁场 $\boldsymbol{B}_0$ 中，核自旋磁矩 $\boldsymbol{\mu}$ 的能量为：

$$E=-\boldsymbol{\mu}\cdot\boldsymbol{B}_0 = -\mu_x B_{0x} -\mu_y B_{0y} -\mu_z B_{0z}$$

通常令外磁场 $\boldsymbol{B}_0$ 平行于 $z$ 轴，上式可化简为：

$$E = - \mu_{z}B_{0}$$

将式 (2) 代入上式，得：

$$E = - \gamma m \hbar B_{0}$$

相邻能级之间的能量差为：

$$\Delta E = \gamma \hbar B_{0}$$

由此可见，外加磁场越大，相邻能级之间的能量差也越大。

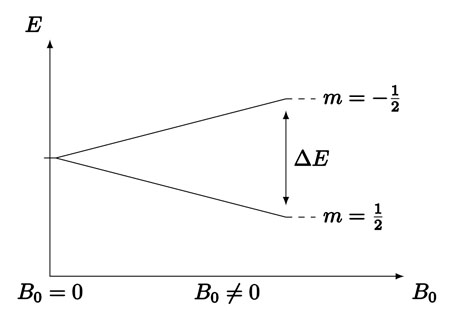
对自旋量子数为 $\frac{1}{2}$ 的原子核，如 $^1\mathrm{H}$ 核，具有两个自旋状态 $m = \frac{1}{2}$ 和 $m = - \frac{1}{2}$。如果旋磁比 $\gamma > 0$，态 $m = - \frac{1}{2}$ 的能量要大于态 $m = \frac{1}{2}$ 的能量。

核磁共振

将样品置于恒定的外磁场下，样品的原子核自旋产生的磁场会在外磁场的作用下重新排列，根据波尔兹曼的粒子数能级分布原理，大多数原子核自旋会处于低能级，即自旋方向顺着外加磁场的方向。此时，再施加额外的射频场（高频交变磁场），使得处于低能级的原子核自旋共振跃迁至高能级（即自旋方向逆着外加磁场的方向），再回到低能级并释放射频信号。这一过程会使外加射频场的能量发生变化，该变化的过程是可以检测的。这就是核磁共振的基本原理。

拉莫尔进动

一个高速旋转的陀螺，当自转轴与重力方向不平行时，其自转轴会绕着重力方向缓慢旋转，这种现象被称为进动。同样的，将一个原子核置于恒定的外加磁场中，若原子核的自旋磁矩与外加磁场方向不同，则原子核磁矩会绕外磁场方向旋转发生进动，这一现象被称为拉莫尔进动。外加磁场 $\boldsymbol{B}_0$ 对核自旋磁矩 $\boldsymbol{\mu}$ 施加了一个力矩 $\boldsymbol{\tau}$：

$$\boldsymbol{\tau} = \boldsymbol{\mu} \times \boldsymbol{B}_0 = \gamma \boldsymbol{S} \times \boldsymbol{B}_0$$

力矩的作用也会影响自旋角动量，即：

$$\boldsymbol{\tau} = \frac{\mathrm{d}\boldsymbol{S}}{\mathrm{d}t}$$

由上两式可得核自旋磁矩在外加磁场作用下的运动方程：

$$\frac{\mathrm{d}\boldsymbol{S}}{\mathrm{d}t} = \gamma \boldsymbol{S} \times \boldsymbol{B}_0 \stackrel{\boldsymbol{\mu} = \gamma \boldsymbol{S}}{\Longrightarrow} \frac{\mathrm{d}\boldsymbol{\mu}}{\mathrm{d}t} = \gamma \boldsymbol{\mu} \times \boldsymbol{B}_0$$

求解这个方程便可得到核自旋磁矩 $\boldsymbol{\mu}$（或自旋角动量 $\boldsymbol{S}$）绕着外磁场 $\boldsymbol{B}_0$ 的方向以一定角频率进动。该频率被称为拉莫尔频率 $\omega$：

$$\omega_L = \gamma B_0$$

将角频率转换为频率，有：

$$ \nu_L = \frac{\omega_L}{2\uppi} = \frac{\gamma B_0}{2\uppi}$$

拉莫尔频率由外加磁场的强度和原子核本身的性质决定。因此，对于某一特定原子，在一定强度的的外加磁场中，其原子核自旋进动的频率是固定不变的。

共振跃迁

对原子核在$z$方向上施加恒定外磁场 $\boldsymbol{B}_0$，再添加一个方向与 $\boldsymbol{B}_0$ 垂直的射频场（高频交变磁场）$\boldsymbol{B}_1$。当射频场的角频率 $\omega$ 等于拉莫尔频率 $\omega_L$ 时，射频场 $\boldsymbol{B}_1$ 对进动中的核自旋磁矩 $\boldsymbol{\mu}$ 的作用相当于恒定磁场，使得核自旋磁矩 $\boldsymbol{\mu}$ 绕着射频场 $\boldsymbol{B}_1$ 发生进动。此时，核自旋磁矩的能量状态发生改变，核自旋磁矩与射频场之间产生能量交换。当射频场的角频率 $\omega$ 不等于拉莫尔频率 $\omega_L$ 时，射频场 $\boldsymbol{B}_1$ 对进动中的核自旋磁矩 $\boldsymbol{\mu}$ 的作用不再相当于恒定磁场，核自旋磁矩 $\boldsymbol{\mu}$ 无法绕着射频场 $\boldsymbol{B}_1$ 发生进动，自旋磁矩的能量状态不发生改变，与射频场没有能量交换。根据磁偶极跃迁的选择定则 $\Delta m = \pm 1$，只有相邻能级间的跃迁才是允许的。根据玻尔频率定则，光子能量与相邻能级的能量差相等时，才会发生跃迁。在这里，当射频光子的能量等于相邻能级的能量差时，原子核发生共振跃迁。由此可知，核磁共振的条件为：

$$\Delta E = \gamma \hbar B_{0} = \hbar \omega \Rightarrow \omega = \gamma B_{0} = \omega_L$$

即射频场角频率等于拉莫尔频率时，才能引起共振跃迁。

共振信号的探测

在这里介绍两种能够使外加射频场能量状态变化的方法。需要注意的是，两种探测方法均为是连续法。连续法的频率分辨率低，而且不能测量驰豫时间，所以这种方法不太常用。另一种探测方法是脉冲法，这种方法分辨率高，可以测量驰豫时间，因此应用广泛。

扫频法

固定磁场 $\boldsymbol{B}_0$，连续改变射频场 $\boldsymbol{B}_1$ 的频率。当射频场 $\boldsymbol{B}_1$ 的角频率 $\omega = \omega_L = \gamma B_{0}$ 时，发生共振跃迁，出现共振峰。

扫场法

固定射频场 $\boldsymbol{B}_1$ 的频率，在共振磁场强度附近连续改变磁场 $\boldsymbol{B}_0$ 的场强（即连续改变相邻能级间的能量差），使扫磁场 $\boldsymbol{B}_0$ 过共振点。这种方法需要在平行于静磁场的方向上叠加一个较弱的交变磁场，该磁场被称为扫场。在连续改变磁场 $\boldsymbol{B}_0$ 的场强时，应缓慢地通过共振点。在这里，缓慢是相对于原子核的驰豫时间而言的。

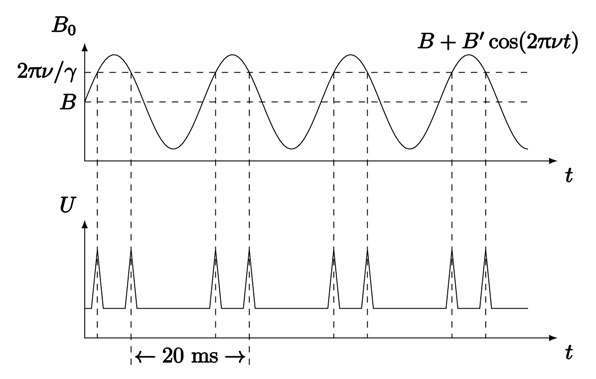
图 2 给出了扫场频率为 50 Hz 时，外磁场随时间的变化及相应的共振信号的关系。从图中可知道，磁场 $\boldsymbol{B}_0$ 的场强变化范围是 $B_0 = B \pm B^\prime $，相邻能级间的能量差也在相应地发生变化。改变射频频率 $\nu$，使 $\nu$ 对应的磁场强度 $B_1$ 在磁场 $\boldsymbol{B}_0$ 的场强变化范围内，就能发生共振。这时的共振信号的间隔可能是不等的，如果继续调整频率 $\nu$，使得共振信号等间距排列，此时扫场不参与共振，便可确定固定磁场 $\boldsymbol{B}_0$ 的场强。

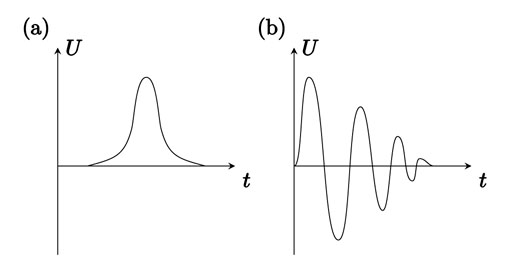
对水来说，50 Hz 的扫场频率是一个变化较快的磁场，观察到的不再是单纯的吸收信号，而会产生拖尾现象。磁场越均匀，尾波中振荡次数越多，拖尾现象越显著。相对而言，纯水的驰豫时间太长（约为 2 s），原子核都被抽运到高能级并达到饱和，以至再次扫过共振点时，低能级不再有大量的原子核可以被抽运。因此，如果水的样品非常纯，共振信号会很小，甚至看不到共振信号，能量的变化便难以检测。此时，可以在水中掺入一些离子，用来减少样品的驰豫时间，以便得到较强的共振信号。

参考文献

本文所引用的内容未能在文中逐一标注，敬请谅解。本文内容参考了以下文献：