四探针测量技术，又称为开尔文测量法，是一种电阻抗测量技术，它使用单独的一对电流和电压探针，测量结果比更简单和更常见的两探针测量法更精确。四探针常被用于测量半导体薄膜的电阻率与方块电阻。

基本方法

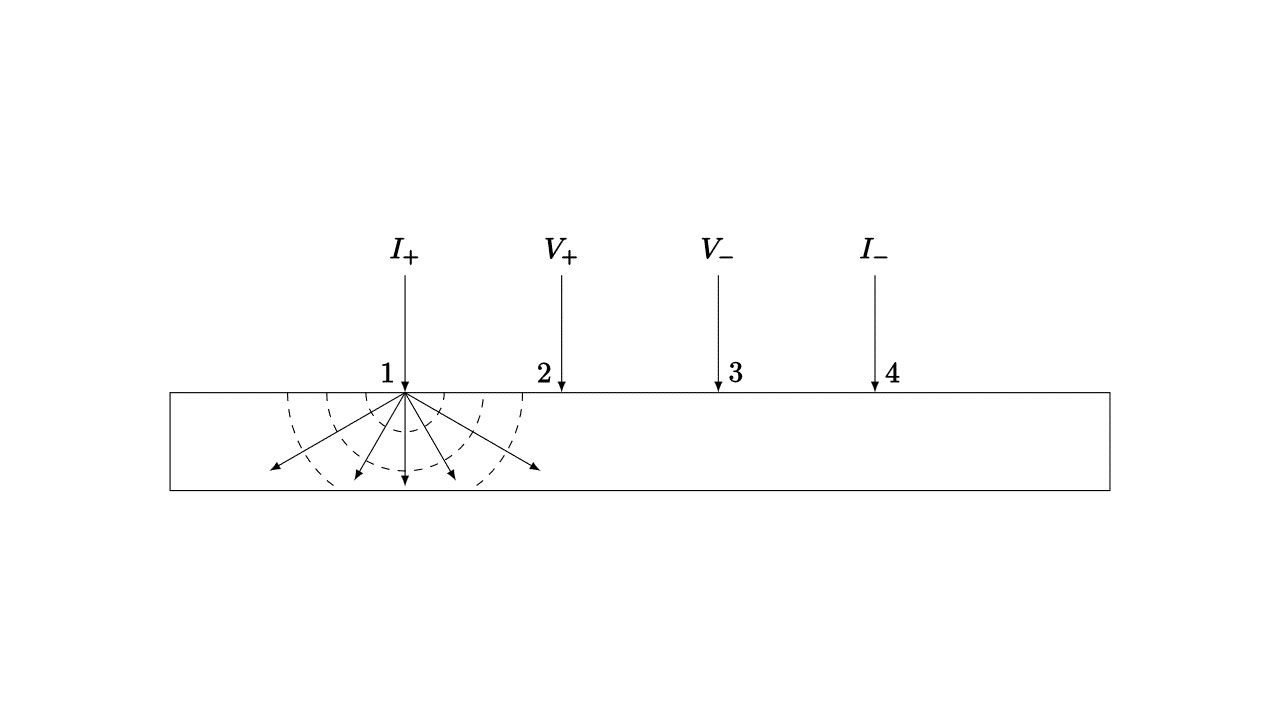
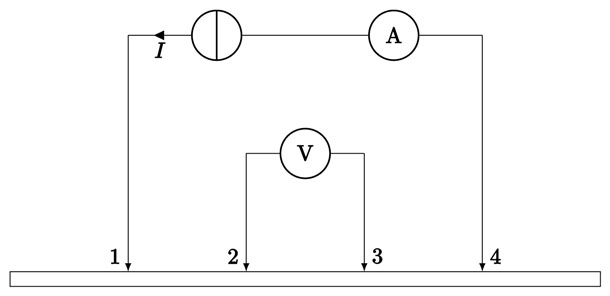
如图 1 所示，四根等间距探针（1、2、3、4）竖直的排成一排，同时施加适当的压力使其与被测样品表面形成欧姆连接，用恒流源给两个外探针（1、4）通以小电流，精准电压表测量内侧两探针（2、3）间电压。根据测量方式和样品的尺寸不同，选取不同的公式计算样品的电阻、电阻率与方块电阻。

样品的测量

在本节中，样品根据其厚度，被简化为大厚度半无穷大样品与半无穷大薄膜样品两种模型。在测量不同厚度的样品时，应使用其对应的测量模型。

大厚度半无穷大样品

电阻 $R$ 与电阻率 $\rho$ 间的关系为：

$$ R = \frac{\rho L}{S} $$

式中，$L$ 为材料的长度，$S$ 为面积。四探针对半导体表面的接触均为点接触，所以对半无穷大样品，电流 $I$ 是以探针尖为圆心呈径向放射状流入体内的，因而电流在体内所形成的等位面为半球面，如图 2 所示。

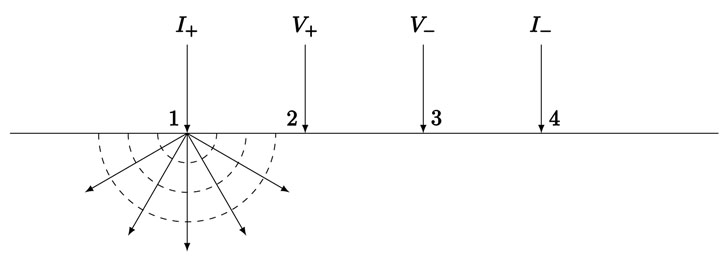
于是，样品电阻率为 $\rho$，半径为 $r$，间距为 $\mathrm{d}r$ 的两个半球等位面间的电阻为：

$$\mathrm{d}R = \frac{\rho}{2\uppi r^2}\ \mathrm{d}r$$

它们之间的电位差为：

$$\mathrm{d}V = I\ \mathrm{d}R = \frac{\rho I}{2\uppi r^2}\ \mathrm{d}r$$

考虑样品为半无限大，在 $r\rightarrow\infty$ 处的电位为 0，所以流经探针 1 的电流 $I$ 在 $r$ 点形成的电位为：

$$(V_r)_1 = \int_{r}^{\infty} \frac{\rho I}{2\uppi r^2} ,\mathrm{d}r = \frac{\rho I}{2\uppi r}$$

流经探针 1 的电流在 2、3 两探针间形成的电位差为：

$$(V_{23})_1 = \frac{\rho I}{2\uppi}\left(\frac{1}{r_{12}}-\frac{1}{r_{13}}\right)$$

流经探针 4 的电流与流经探针 1 的电流方向相反，所以流经探针 4 的电流 $I$ 在探针 2、3 之间引起的电位差为：

$$(V_{23})_4 = -\frac{\rho I}{2\uppi}\left(\frac{1}{r_{42}}-\frac{1}{r_{43}}\right)$$

于是流经探针 1、4 之间的电流在探针 2、3 之间形成的电位差为：

$$V_{23} = \frac{\rho I}{2\uppi}\left(\frac{1}{r_{12}}-\frac{1}{r_{13}}-\frac{1}{r_{42}}+\frac{1}{r_{43}}\right)$$

由此可得样品的电阻率为：

$$\rho = \frac{2\uppi V_{23}}{I}\left(\frac{1}{r_{12}}-\frac{1}{r_{13}}-\frac{1}{r_{42}}+\frac{1}{r_{43}}\right)^{-1}$$

此式就是四探针法测半无限大样品电阻率的普遍公式。在采用四探针测量电阻率时通常使用图等间距直线形结构，假设直线四探针的探针间距均为 $s$，则对于直线四探针有：

$$\rho = \frac{2\uppi s V_{23}}{I} = \frac{CV_{23}}{I}$$

式中，$C=2\uppi s$ 为探针系数。需要注意的是，此式只适用于厚度很大（样品厚度 $t > 4s$ ）的半无限大体材料。由于块状和棒状样品外形尺寸（ $t > 4 \ \mathrm{mm}$ ）与探针间距比较，合乎于半无限大的边界条件，或者当探头的任一探针到样品边缘的最近距离不小于 $4s$ 时，测量区的电阻率值可以直接由上式得出。当样品厚度和直径为有限大时，需要乘上修正因子。根据样品厚度 $t$ 和直径 $d$ 修正后的体电阻率为：

$$\rho = F_1\left(\frac{t}{s}\right) \cdot F_2\left(\frac{d}{s}\right) \cdot \frac{C V_{23}}{I}$$

式中，$F_1\left(\frac{t}{s}\right)$ 为厚度修正因子，$F_2\left(\frac{d}{s}\right)$ 为样品边缘与测试位置修正因子，这两个因子可以通过查表得到。

半无穷大薄膜样品

半无限大薄膜样品上探针电流的分布及等势面如图 3 所示。

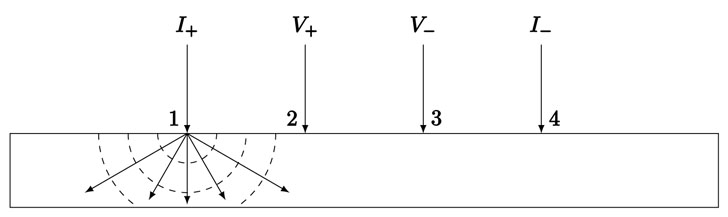
当样品厚度 $t \ll s$ 时，可以将等电位面近似看成是一个圆柱面，高为 $t$，圆柱底面半径为 $r$，则等电位面的面积为：

$$A = 2\uppi r t$$

样品电阻率为 $\rho$，半径为 $r$，间距为 $\mathrm{d}r$ 的两个半球等位面间的电阻为：

$$\mathrm{d}R = \frac{\rho}{A}\ \mathrm{d}r$$

它们之间的电位差为：

$$\mathrm{d}V = I\ \mathrm{d}R = \frac{\rho I}{A}\ \mathrm{d}r$$

探针 1 的电流在 2、3 两探针间形成的电位差为：

$$(V_{23})_1 = \frac{\rho I}{2\uppi t} \cdot \ln \frac{r_{13}}{r_{12}} = \frac{\rho I}{2\uppi t} \cdot \ln 2$$

探针 4 的电流 $I$ 在探针 2、3 之间引起的电位差为：

$$(V_{23})_4 = -\frac{\rho I}{2\uppi t} \cdot \ln \frac{1}{2}$$

于是探针 2、3 之间形成的总电位差为

$$V_{23} = \frac{\rho I}{\uppi t} \cdot \ln 2$$

可得电阻率为：

$$\rho = \frac{\uppi t }{\ln 2} \cdot \frac{V_{23}}{I}$$

方块电阻是一个正方形的薄膜导电材料边到边之间的电阻。它的定义式为：

方块电阻几何变量定义如图 4 所示：

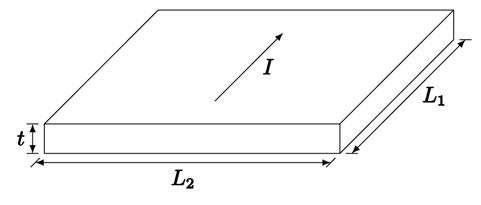
方块电阻与电阻的关系式为：

$$R = R_\Box \cdot \frac{L_1}{L_2}$$

式中，$L_1$ 应与电流方向平行，$L_2$ 应与 $L_1$ 垂直。 由式 (1) 可得半无限大薄膜样品的方块电阻为：

$$R_\Box = \frac{\uppi}{\ln 2} \cdot \frac{V_{23}}{I} = k \cdot \frac{V_{23}}{I}$$

式中，系数 $k=\uppi/\ln 2$。方块电阻的常用单位为欧姆每方，写作 $\Omega/\Box$ 或 $\Omega/\mathrm{sq}$。方块电阻有一个特性，即任意大小的正方形边到边的电阻都是一样的，方块电阻仅与导电膜的厚度和电阻率有关。需要注意的是，上式只适用于样品厚度非常薄（ $t \ll s$ ）的半无限大二维（薄膜）材料。当样品厚度 $t$ 与 $s$ 相当或者直径 $d$ 为有限大时，需要将系数 $k$ 替换为厚度修正因子 $k_1\left(\frac{t}{s}\right)$ 与直径修正因子 $k_2\left(\frac{d}{s}\right)$ 的乘积进行修正，即：

$$R_\Box = k_1\left(\frac{t}{s}\right) \cdot k_2\left(\frac{d}{s}\right) \cdot \frac{V_{23}}{I}$$

薄片样品（ $t ≤ 4 \ \mathrm{mm}$ ）因为其厚度与探针间距比较不能忽略，测量时要提供样品的修正因子，可以通过查表得到。利用上式与式 (1) ，结合测量结果，便可求得样品的方块电阻与电阻率。

参考文献

本文所引用的内容未能在文中逐一标注，敬请谅解。本文内容参考了以下文献：